What Happens to a Hockey Puck When a Net Force of 5 N Acts on It?

Newton's Laws of Motility Review

Navigate to:

Review Session Home - Topic List

Newton's Laws - Home  ||  Printable Version  ||  Questions with Links

Answers to Questions:  All  ||  #1-7  ||  #8-36  ||  #37-46  ||  #47-60

[ #47 |#48 |#49 |#fifty |#51 |#52 |#53 |#54 |#55 |#56 |#57 |#58 |#59 |#60 ]

Role F: Trouble Solving

For the following problems, depict gratuitous-body diagrams and solve for the requested unknown. Usechiliad = 9.8 m/southward/southward.

The following links may pb to useful data for questions #47-threescore:

47. A 0.250-kg ball is thrown up with an initial velocity of 12.0 m/s at an angle of 30.0 degrees. Decide the dispatch of the ball when it has reached the peak of its trajectory. Assume negligible air resistance.PSYW

Answer: nine.viii thou/south/south, down

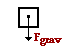At that place is simply i force upon the brawl - the force of gravity. (Air resistance is negligible; the brawl is not on a surface, and then in that location is no friction or normal strength; the practical force which projects information technology into motility does not act upon the ball during its trajectory; there are no springs, strings, wires, or cables attached so in that location is neither a tension force nor a spring force.) The force of gravity acts down with a magnitude of m•m = (0.250 kg) •(ix.8 one thousand/s/s) = 2.45 N. The net strength is two.45 North; when divided past mass, the acceleration tin can exist establish.

 a = F_net / m = (ii.45 Northward, downwardly) / (0.250 kg) = 9.8 thou/s/s, down

[ #47 |#48 |#49 |#l |#51 |#52 |#53 |#54 |#55 |#56 |#57 |#58 |#59 |#60 ]

48. A 72-kg skydiver is falling from 10000 feet. At an instant during the fall, the skydiver encounters an air resistance force of 540 Newtons. Decide the dispatch of the skydiver at this instant.PSYW

Reply: 2.3 grand/due south/s, down

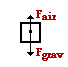There are two forces acting upon the skydiver - gravity (down) and air resistance (up).  The strength of gravity has a magnitude of m•thousand = (72 kg) •(ix.8 m/s/s) = 706 N. The sum of the vertical forces is

∑ F_y = 540 North, up + 706 N, down = 166 North, down

The acceleration of the skydiver can exist computed using the equation ∑ F_y = one thousand•a_y.

a_y = (166 Northward, downwards) / (72 kg) = 2.3 grand/s/due south, down

[ #47 |#48 |#49 |#l |#51 |#52 |#53 |#54 |#55 |#56 |#57 |#58 |#59 |#lx ]

49. A 72-kg skydiver is falling from ten 000 anxiety. Later reaching concluding velocity, the skydiver opens his parachute. Shortly thereafter, in that location is an an instant in time in which the skydiver encounters an air resistance force of 1180 Newtons. Determine the acceleration of the skydiver at this instant.PSYW

Answer: 6.half-dozen m/s/south, up

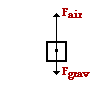There are two forces interim upon the skydiver - gravity (downwardly) and air resistance (upward). The force of gravity has a magnitude of 1000•g = (72 kg) •(ix.8 1000/s/s) = 706 N. The sum of the vertical forces is

∑ F_y = 1180 N, upwardly + 706 N, down = 474 N, up

The acceleration of the skydiver tin can be computed using the equation ∑ F_y = 1000•a_y.

a_y = (474 Northward, up) / (72 kg) = 6.6 g/s/s, up

[ #47 |#48 |#49 |#fifty |#51 |#52 |#53 |#54 |#55 |#56 |#57 |#58 |#59 |#60 ]

fifty. A v.xx-N force is practical to a 1.05-kg object to accelerate it rightwards beyond a friction-complimentary surface. Determine the acceleration of the object. (Fail air resistance.)PSYW

Answer: 4.95 m/south/s, right

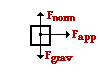Upon neglecting air resistance, at that place are three forces acting upon the object. The up and down strength balance each other and the dispatch is caused by the applied force. The net strength is 5.20 Due north, right (equal to the only rightward forcefulness - the applied force). So the acceleration of the object can be computed using Newton'southward second law.

a = F_internet / m = (v.xx Northward, right) / (one.05 kg) = 4.95 m/southward/s, correct

[ #47 |#48 |#49 |#fifty |#51 |#52 |#53 |#54 |#55 |#56 |#57 |#58 |#59 |#60 ]

51. A 5.20-Northward force is applied to a 1.05-kg object to advance it rightwards. The object encounters 3.29-N of friction. Determine the acceleration of the object. (Neglect air resistance.)PSYW

Respond: 1.82 one thousand/s/southward, right

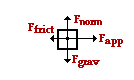Upon neglecting air resistance, there are iv forces acting upon the object. The up and down forces remainder each other. The acceleration is rightward since the rightward applied force is greater than the leftward friction force. The horizontal forces can be summed as vectors in order to determine the internet strength.

F_internet = ∑F_x = 5.20 North, right - iii.29 N, left = ane.91 Due north, correct

The acceleration of the object can be computed using Newton's second law.

a₁₀ = ∑ F_x / m = (one.91 N, down) / (one.05 kg) = i.82 1000/s/southward, right

[ #47 |#48 |#49 |#fifty |#51 |#52 |#53 |#54 |#55 |#56 |#57 |#58 |#59 |#lx ]

52. Determine the applied force required to accelerate a three.25-kg object rightward with a abiding acceleration of ane.twenty m/s/south if the force of friction opposing the motion is 18.2 Due north. (Neglect air resistance.)PSYW

Reply: 22.1 North

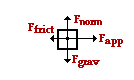There are four forces acting upon the object equally shown in the costless-body diagram at the right. The two vertical forces must balance since there is no vertical acceleration. Since the mass and the dispatch are known, the net force can exist computed:

F_net = g•a = (3.25 kg, right) • (1.20 k/s/s) = 3.90 North, right

Since the dispatch is to the right, the net force is directed to the right. Thus, the rightward forcefulness (practical force) must exceed the leftward strength (friction strength) by an corporeality equal to the 3.9 Due north. Then the practical force tin exist computed.

F_app = F_frict + F_net = 18.2 N + three.ninety N = 22.ane N

[ #47 |#48 |#49 |#50 |#51 |#52 |#53 |#54 |#55 |#56 |#57 |#58 |#59 |#sixty ]

53. A 921-kg sports automobile is moving rightward with a speed of 29.0 m/southward. The commuter suddenly slams on the brakes and the car skids to a stop over the course of 3.20 seconds with the wheels locked. Make up one's mind the average resistive force interim upon the car.PSYW

Respond: 8350 N

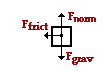In that location are three (peradventure four) forces acting upon this motorcar. There is the upward force (normal force) and the downward force (gravity); these 2 forces balance each other since there is no vertical dispatch. The resistive force is likely a combination of friction and air resistance. These forces deed leftward upon a rightward skidding auto. In the gratis-trunk diagram, these 2 forces are represented by the F_frict arrow.

The acceleration is non given but can be calculated from the kinematic information that is given:

five_i = 29.0 m/due south, v_f = 0 m/s, and t = 3.20 s

The acceleration of the object is the velocity change per fourth dimension:

a = Delta v / t = (0 thousand/s - 29.0 thou/s) / (iii.20 s) = -nine.67 chiliad/southward/south or 9.67 m/s/south, left.

This acceleration can be used to make up one's mind the net force:

F_net = k•a = (921 kg) • (9.67 yard/due south/southward, left) = 8350 N, left

The friction forces (surface and air) provide this net forcefulness and are equal in magnitude to this internet force.

[ #47 |#48 |#49 |#l |#51 |#52 |#53 |#54 |#55 |#56 |#57 |#58 |#59 |#lx ]

54. A 0.250-kg rightward moving air track glider decreases its speed from 0.872 k/s to 0.798 m/s over the length of a one.71-grand long air track. Make up one's mind the average resistive force acting upon the air track glider.PSYW

Answer: 0.00903 N

This problem is similar to the previous problem. There are iii (and perhaps 4) forces interim upon the glider. The up strength could exist considered to be a normal strength or an air resistance force (from the air blowing through the air track holes). Similar the previous problem, the dispatch is not given but it can be calculated from the kinematic information:

v_i = 0.872 m/s, v_f = 0.798 yard/south, and d = i.71 thou

Using a kinematic equation, the values for initial and concluding velocity and deportation can be substituted; the algebraic steps are shown below.

v_f ⁱⁱ = v_i ² + 2•a•d

(0.872 m/s)^two = (0.798 grand/southward)² + ii•a•(1.71 m)

(0.872 m/due south)² - (0.798 m/south)^two = 2•a•(ane.71 m)

0.124 m²/due southⁱⁱ = (3.42 m)•a

0.0361 1000/south/due south = a

This acceleration tin exist used to make up one's mind the net strength:

F_net = m•a = (0.250 kg) • (0.0361 thousand/s/southward, left) = 0.00903 Northward, left

The friction forces (surface and air) provide this net force and are equal in magnitude to this net forcefulness.

[ #47 |#48 |#49 |#l |#51 |#52 |#53 |#54 |#55 |#56 |#57 |#58 |#59 |#lx ]

55. A 1250-kg minor aircraft decelerates along the track from 36.6 1000/due south to half dozen.80 m/s in 5.10 seconds. Determine the average resistive force interim upon the plane. (Assume that its engine/propeller makes no contributes to its frontwards movement).PSYW

Answer: seven.thirty 10 10³ N

This problem is similar to the two previous problems in many respects: the complimentary-trunk diagram is identical or similar and the acceleration is not given but determinable from the kinematic data.

v_i = 36.half-dozen m/south, five_f = half-dozen.80 thousand/s, and t = five.10 s

The dispatch of the object is the velocity change per time:

a = Delta 5 / t = (6.80 yard/due south - 36.6 g/southward) / (5.10 s) = -5.84 m/s/due south or v.84 m/s/s, left.

This acceleration tin be used to determine the net force:

F_net = thou•a = (1250 kg) • (5.84 thou/s/s, left) = seven.30 ten 10³ North, left

The friction forces (surface and air) provide this cyberspace force and are equal in magnitude to this cyberspace strength.

[ #47 |#48 |#49 |#50 |#51 |#52 |#53 |#54 |#55 |#56 |#57 |#58 |#59 |#lx ]

56. A tow truck exerts a 18300-Northward strength upon a 1210 car to drag information technology out of a mud puddle onto the shoulder of a road. A 17900 N force opposes the automobile's motility. The plane of movement of the automobile is horizontal. Decide the fourth dimension required to drag the machine a altitude of vi.90 meters from its rest position.PSYW

Answer: half dozen.46 s

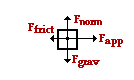Upon neglecting air resistance, there are four forces acting upon the object. The up and down forces residuum each other. The dispatch is rightward (or in the direction of the applied strength) since the rightward applied forcefulness is greater than the leftward friction forcefulness. The horizontal forces can be summed as vectors in order to determine the net force.

F_net = ·F_x = 18300 North, correct - 17900 North, left = 400 Due north, correct

The acceleration of the object can be computed using Newton's second law.

a₁₀ = ·F_x / m = (400 North, downward) / (1210 kg) = 0.3306 m/due south/s, right

This acceleration value can exist combined with other known kinematic information (v_i = 0 yard/s, d = half-dozen.ninety m) to determine the time required to drag the car a distance of vi.ix m. The following kinematic equation is used; substitution and algebra steps are shown.

d = 5_i • t + 0.5 •a • t²

d = five_i • t + 0.v •a • t²

half-dozen.90 thou = 0.5 • (0.3306 m/s/southward) • tⁱⁱ

6.90 k / (0.v • 0.3306 grand/s/s ) = t²

41.4 = t²

6.46 s = t

[ #47 |#48 |#49 |#50 |#51 |#52 |#53 |#54 |#55 |#56 |#57 |#58 |#59 |#60 ]

57. A four.44-kg bucket suspended past a rope is accelerated upwards from an initial rest position. If the tension in the rope is a constant value of 83.1 Newtons, then decide the speed (in m/s) of the bucket later on i.59 seconds.PSYW

Answer: 14.2 1000/s

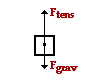At that place are two forces acting upon the bucket - the forcefulness of gravity (up) and the tension force (downwards). The magnitude of the strength of gravity is found from m•g; its value is 43.5 N. These two forces tin be summed every bit vectors to determine the internet forcefulness.

F_net = ·F_y = 83.1 Due north, upwards + 43.5 North, down = 39.half-dozen N, up

The acceleration can be calculated using Newton's 2nd law of motion.

a = F_net / m = (39.vi N, up) / (4.44 kg) = 8.92 m/due south/southward, up

The acceleration value tin can be used with other kinematic information (v_i = 0 thou/s, t = 1.59 s) to calculate the terminal speed of the bucket. The kinematic equation, substitution and algebra steps are shown.

v_f = v_i + a•t

v_f = 0 g/southward + (8.92 m/southward/s)•(1.59 southward)

5_f = fourteen.2 m/s

[ #47 |#48 |#49 |#l |#51 |#52 |#53 |#54 |#55 |#56 |#57 |#58 |#59 |#lx ]

58. A 22.6-Northward horizontal force is applied to a 0.0710-kg hockey puck to advance it across the water ice from an initial rest position. Ignore friction and determine the final speed (in thou/s) of the puck after existence pushed for a time of .0721 seconds.PSYW

Answer: 23.0 k/s

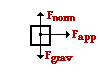Upon neglecting air resistance, in that location are three forces acting upon the object. The up and down force balance each other and the acceleration is caused past the applied strength. The cyberspace force is 22.vi N, right (equal to the only rightward forcefulness - the practical force). And then the acceleration of the object tin be computed using Newton's second law.

a = F_internet / m = (22.6 N, right) / (0.0710 kg) = 318 k/due south/south, correct

The acceleration value can be used with other kinematic information (v_i = 0 m/south, t = 0.0721 s) to calculate the final speed of the puck. The kinematic equation, commutation and algebra steps are shown.

v_f = 5_i + a•t

v_f = 0 m/s + (318 m/s/s)•(0.0721 s)

5_f = 23.0 thou/s

[ #47 |#48 |#49 |#50 |#51 |#52 |#53 |#54 |#55 |#56 |#57 |#58 |#59 |#lx ]

59. A train has a mass of 6.32x10⁴ kg and is moving with a speed of 94.three km/60 minutes. The engineer applies the brakes which results in a net backward force of 2.43x10^v Newtons on the train. The brakes are held for 3.40 seconds. How far (in meters) does the train travel during this fourth dimension?PSYW

Reply: 66.8 m

At that place are three (perhaps four) forces acting upon this train. There is the upward force (normal strength) and the downward force (gravity); these two forces balance each other since in that location is no vertical acceleration. The resistive force is likely a combination of friction and air resistance. These forces act leftward upon a rightward skidding railroad train. In the free-body diagram, these 2 forces are represented by the F_frict pointer. The value of this resistive forcefulness is given as ii.43x10^v N. This is the cyberspace force since at that place are no other horizontal forces; it is the force which causes the acceleration of the train. The acceleration value can be determined using Newton's second police force of movement.

a = F_net / one thousand = (2.43x10^v N) / (vi.32x10^four kg) = 3.84 m/s/s, left

This acceleration value can be combined with other kinematic variables (vi = 94.3 km/hr = 26.ii m/due south; t = 3.forty southward) in order to determine the altitude the train travels in 3.4 seconds.

d = v_i • t + 0.5 •a • t²

d = (26.2 thou/s) • (iii.forty s) + 0.5 • (-iii.84 m/southward/s) • (3.40 s)^two

d = 89.1 m - 22.2 m

d = 66.8 m

[ #47 |#48 |#49 |#50 |#51 |#52 |#53 |#54 |#55 |#56 |#57 |#58 |#59 |#threescore ]

60. A shopper in a supermarket pushes a loaded cart with a horizontal force of 16.5 Newtons. If the cart has a mass of 33.8 kg, how far (in meters) volition it move in ane.31 seconds, starting from residuum? (Neglect resistive forces.)PSYW

The following links may lead to useful information for Questions #47-60:

Reply: 0.419 m

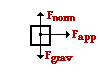Upon neglecting air resistance, there are three forces acting upon the object. The upwards and down force balance each other and the dispatch is caused by the applied force. The internet force is 22.6 Due north, correct (equal to the only rightward force - the applied forcefulness). So the acceleration of the object can be computed using Newton's second police.

a = F_net / 1000 = (16.five North, right) / (33.8 kg) = 0.488 thousand/s/s, right

The dispatch value can be used with other kinematic information (v_i = 0 g/s, t = i.31 s) to calculate the concluding speed of the cart. The kinematic equation, substitution and algebra steps are shown.

d = five_i • t + 0.v •a • t²

d = v_i • t + + 0.5 • (0.488 one thousand/s/s)•(1.31 s) ²

d = 0.419 yard

[ #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ]

Navigate to:

Review Session Home - Topic Listing

Newton'south Laws - Domicile  ||  Printable Version  ||  Questions with Links

Answers to Questions:  All  ||  #1-7  ||  #8-36  ||  #37-46  ||  #47-60

You Might Likewise Similar ...

Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and didactics. If that is what you're looking for, then you lot might also like the following:

1. The Calculator Pad

   The Figurer Pad includes physics discussion problems organized by topic. Each trouble is accompanied by a popular-up answer and an sound file that explains the details of how to arroyo and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.

   Visit: The Calculator Pad Habitation | Figurer Pad - Newton's Laws

2. Minds On Physics the App Series

   Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the pupil that is serious almost improving their conceptual understanding of physics. Each module of the serial covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like surroundings. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 2 of the serial includes Newton'south Laws of Motion.

   Visit: MOP the App Home || MOP the App - Part 2

sutherlandfromends68.blogspot.com

Source: https://www.physicsclassroom.com/reviews/Newtons-Laws/Newtons-Laws-Review-Answers-4

Share this post